Counting Liberties

British Go Journal No. 11. March 1970. Page 13.

Part 2

Masayoshi Fukuda, 6p

In the previous article we saw how the table:
3 4 5 6
3 5 8 12
gave the number of liberties of a group of stones with enemy stones inside it which can be captured. Remember that the formula applies immediately after the enemy stones have been captured. In this concluding article we will see how the table may be applied to other positions, and some positions where it cannot be applied without modification.

Diagrams 4a, b & c

How about the position in Dia 4a? Black has been fighting furiously, and dares not let the position be resolved in whites favour, but a play at another part of the board is desperately needed too. Does he dare tenuki? It would be an unusual beginner who could be sure without knowing the 5:8 rule. If he does know the rule, he can play elsewhere with confidence; the whites including the marked stone have nine liberties, but black has ten, one more than enough. We arrive at the count of ten as follows: if both were occupied by white stones, the black chain would have eight liberties, as shown by the table, but 'a' and 'b' obviously constitute two additional liberties, just as vacant points do for a simple chain. Observe that we must mentally discount one outside and one inside point (the points) in order to compare the position with those for which the table was calculated.

In Dia 4b, we meet a new refinement. If we mentally erase the Black stone, we can imagine that the surrounded White chain has just been forced to take four Black stones which had formed an inner square. At that moment the White stones had, from the table, five liberties. But Black has already played inside, at the marked stone, so White has been cut down from five to four liberties. Since the Black stones to the right have four liberties, first play wins in this situation.

Perhaps the situation did not arise in this way - there probably never were four Black stones inside. We shall not let the previous history of a position prevent us from recognising a situation where we can easily count the liberties!

Similarly in Dia 4c we are called on to recognise through its disguise one of the forms we have become familiar with. We can recognise the situation as one equivalent to two plays later than the capture of six White stones, and therefore we can count twelve minus two is ten liberties for Black. The White stones above have eleven liberties, so White can tenuki, making a play elsewhere that may win the game.

It should be emphasised that situations which involve ko, or where there is a possibility of seki, are not covered in this discussion. Furthermore, the table of captives and liberties does not hold if there is a weakness in the surrounding chain. Nor, and this exception is of great practical importance, does the table always hold in corner situations, as Figure 5 will show.

Diagram 5a, b, c & d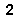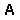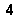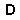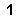

In the corner, the number of liberties depends on the form of the captured group. The position in Dia 5a shows four stones in the corner in the form of a square, which white can capture. Usually this would net him five liberties, so that he would have time to kill the three marked black stones, which have only three liberties. But the special rule for a corner square of four stones is that only three liberties to result. Thus in this particular situation first play wins. The sequence would be, if Black plays first: black 1, white 2 captures 4 stones, black 3 at , white 4 perhaps and black 5 at atari.

Dia 5b, however, although in the corner, follows the 4:5 rule. The black marked stones have five liberties, the four captives in the corner lead to five liberties just as they would elsewhere, and first play wins the situation.

Diagram 5e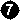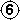

In Dia 5c white can capture the five blacks in the corner, but here, instead of eight, he gains only four liberties, and first play wins this situation, as the marked black stones also have four liberties. The sequence after a black play at 1 and the white reply at 2 capturing 5 in Diagram 5b, is shown in Diagram 5e.

Dia 5d shows a position where the simple rules of counting do not hold because of a weakness in the surrounding chain. Here the point is of crucial importance. If white is to play, he plays here and wins, since he gains five liberties by the capture of four black stones inside, and the outside black stones have only three liberties. If black plays first, he plays here to atari all the white stones; white captures with and black wins with the sequence shown in Dia 6a.

Diagram 6a & b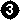

Dia 6b also shows another example of a weakness in the our surrounding chain which complicates the situation.

Diagram 6c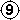

If it is white to play, he must play at 1 in order to win - this is atari, and black must take 5 stones with black at 2 leading to the sequence in Dia 6c.

Diagram 6d

Diagram 6e

If white plays first as in Diagram 6d, he loses: after white 3 in Diagram 6e (to prevent two eyes), black 4! By analogy with previous positions we count seven liberties for black at this point, and, although white could reduce these to six by another inside play, black would not have to answer, since the outside white stones have only five liberties.

We see, then, that knowledge of the rule is valuable in many situations, but that it does not necessarily apply in corners, or when there is a weakness in the surrounding chain. Remember that we have not started to consider situations involving possibilities of ko or seki, and these must be considered on their individual merits.

Concluded.